¿Puedo soñar con una cartera de inversión coherente?

ALICANTE. En el artículo que publicamos el pasado mes de septiembre resaltamos la importancia en asegurar una prelación entre perfiles de riesgo y resultados con el fin de evitar consecuencias negativas a la hora de invertir con un objetivo preestablecido. Avanzamos que existe un método para alcanzar la coherencia buscada y evitar situaciones como las descritas en el ejemplo del artículo. Este método es conocido por muchos, pero aplicado pocas veces a pesar de ser la única forma de garantizar los resultados buscados. 

Para garantizar la coherencia entre riesgo y rentabilidad, todo inversor debería ser recompensado de la misma forma por el riesgo asumido independientemente de su perfil de riesgo. Poniendo un ejemplo, si un inversor dinámico que asume 12 unidades de riesgo obtiene 8 unidades de rentabilidad, entonces un inversor moderado que asume 6 unidades de riesgo debería conseguir una proporción positiva de estas 8 unidades de rentabilidad.

En la Teoría de Carteras, la rentabilidad por unidad de riesgo se puede medir con el Ratio de Sharpe (R.S.). El R.S. se calcula como el cociente entre el exceso de rentabilidad frente al activo libre de riesgo (a.l.r.), y la desviación de las rentabilidades. Si las carteras de distintos inversores con diferentes perfiles de riesgo tienen el mismo R.S., podremos siempre esperar una coherencia entre resultados y el riesgo asumido. La pregunta clave es como construir tales carteras.

En primer lugar, conviene determinar la magnitud del R.S. deseado por el inversor. Seguramente cualquier inversor busca maximizar este ratio, es decir obtener la máxima rentabilidad por unidad de riesgo. De todas las carteras que podemos confeccionar con los activos disponibles en el mercado, solamente existe una única cartera que tiene un R.S. máximo. Esta cartera se identifica por la Cartera de Mercado (C.M.), cartera que se compone de todos los activos existentes ponderados por su presencia en el mercado. Cuando hablamos de activos existentes en el mercado podemos pensar en la renta variable, los instrumentos relacionados con los tipos de interés, el crédito, y los activos inmobiliarios. Todo ello a nivel global y con una ponderación relacionada con su capitalización.

Volatilidad

Una vez identificado la cartera que presenta mejor comportamiento relativo al riesgo cabe preguntarse que características presenta tal cartera. Según estudios a largo plazo, la rentabilidad anual de esta cartera fue del 8,37% con un riesgo del 11,46% (volatilidad). Para que un inversor pueda valorar si tal nivel de riesgo se ajusta a su perfil, podemos enumerar una serie de medidas de riesgo que sean interpretables de forma más directa. 

En el período entre 1960 y 2015, el rango de rentabilidad anual de la C.M. se situó entre el -24,40% y el 35,61%. En los 55 años bajo estudio se obtuvieron rentabilidades negativas en 14 de ellos, dos de los cuales perdiendo más del 10%. La rentabilidad media durante los años con rentabilidad negativa fue del -6,38%.

Aunque la rentabilidad a largo plazo (8,37%) fuera positiva, no todos los inversores están dispuestos a ver caídas de más de 20% en su patrimonio invertido. Pero por otro lado esta cartera es la que maximiza la rentabilidad por unidad de riesgo y por lo tanto sería coherente que todo inversor invirtiese en ella. Nos interesa entonces reducir el riesgo de esta cartera para ajustarla al perfil de cualquier inversor. Normalmente lo que se suele hacer en este caso es aumentar la ponderación de activos de menor riesgo (instrumentos sobre tipos de interés y crédito) en detrimento de los activos de mayor riesgo (renta variable, activos mobiliarios). 

Esto suele ser la solución más utilizada, pero es errónea ya que modifica el R.S. Este es un efecto no deseado ya que como apuntamos anteriormente queremos que el R.S. sea máximo y sabemos que existe una única cartera con tal ratio. No tenemos que olvidarnos que queremos guardar la prelación entre riesgos y resultados, es decir, que el inversor que busca menor riesgo que la que ofrece la C.M., no debería sentirse perjudicada por una rentabilidad desproporcionalmente menor.

Asignación de activos

La solución se encuentra en introducir en la asignación de activos el a.l.r. Por definición el a.l.r. no tiene variabilidad. Si seleccionamos por ejemplo una letra del Tesoro a un año al 2,5% como a.l.r., podemos estar seguros de que nos devolverán nuestra inversión después de un año multiplicado por 1,025. Esto es, ni 0,98, ni 1,04. No hay variabilidad. La rentabilidad obtenida (ex-post) será igual a la rentabilidad esperada (ex-ante). Al no existir variabilidad, el usar en la cartera un a.l.r. no afectará al R.S. al combinarlo con la C.M. Para el R.S., su efecto es neutro. Como efecto positivo sin embargo sí reduce el riesgo de la cartera. De esta forma, variando las proporciones del capital invertido entre la C.M. y el a.l.r., podremos ajustar una cartera a cualquier perfil inversor.

Si seleccionamos la rentabilidad y volatilidad esperada de la C.M. a partir de la rentabilidad y volatilidad observada durante el periodo 1960-2015 y contemplamos para el a.l.r. una rentabilidad del 0,2%, podemos construir las siguientes carteras:

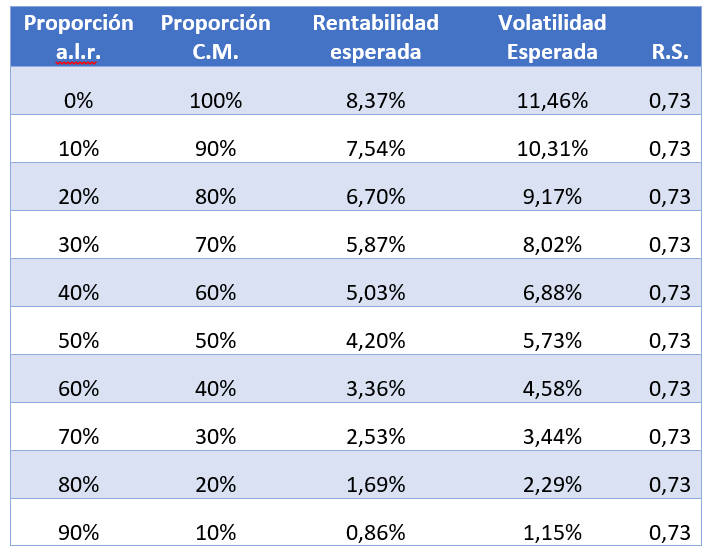
La tabla muestra que a medida que aumentamos la proporción del a.l.r. en detrimento de la C.M. se reduce la volatilidad esperada, de forma que cada inversor podrá ajustar su cartera al perfil de riesgo requerido.

Es importante resaltar que el R.S. se mantiene constante para cada una de las 10 carteras y, por lo tanto, existirá coherencia entre el riesgo asumido y la rentabilidad. Con ello garantizamos que todos los inversores indistintamente de su perfil puedan esperar una recompensa proporcional por el riesgo de su inversión. 

Maximizando la rentabilidad

Como guinda al pastel, no solo alcanzamos la coherencia soñada, sino que las carteras resultantes maximizan la rentabilidad por unidad de riesgo. Ello significa que cualquiera de estas carteras consigue un R.S. superior a toda cartera eficiente que se construye habitualmente variando la proporción entre activos de menor riesgo (instrumentos sobre tipos de interés y crédito) y activos de mayor riesgo (renta variable, activos mobiliarios).  

Hasta el momento solo hemos hablado de la C.M. y del a.l.r. de forma muy genérica. En un futuro artículo describiremos de forma práctica estos dos conceptos y daremos unos consejos para que cualquier inversor pueda aplicar estas ideas a su propia cartera de inversión.

Marc Leutscher es responsable de inversión, producto y riesgo de la EAFI alicantina gCapital Wealth Management